Relativitetsteorin

Före Einsteins upptäckter kring relativitetsteorin så var det Galileis relativitetsteori som gäld. Galilei bestämde denna med hjälp av dåtidens postulat som var dåtidens grunder man trodde sig kunna lita på. Ett par av dessa postulat som sedan Einstein kom att mot bevisa var t.ex. att en sekund eller en meter alltid är lika långa, oavsett vem som mäter. Utifrån dessa postulat kunde man tillslut framställa en teori.

 Denna teori sade tillexempel att om två massor möts, så för att beräkna den enes hastighet jämfört med den andres så adderas hastigheterna. Denna teori utvecklade under 1500-talet fram till 1700-talet med Galilei och Newton som förgrundsfigurer. År 1817 så utförde Albert Michelson och Edward Morley en väldigt exakt mätning av ljusets hastighet som visade att alltid är konstant oberoende av både ljuskällans och betraktarens hastigheter, detta passade inte alls ihop med Galileis relativitetsprincip för enligt denna måste man uppleva en högre hastighet om man åker mot ljusets hastighet än om man åker mot ljuset.

Albert Einstein var den som revolutionerade människans syn på relativiteten i en artikel år 1905 då han beskrev vad Michelson-Morleys experiment egentligen innebar.  Denna beskrivning kom att kallas den speciella relativitetsteorin. Denna teori är den samma som Newtons vid låga hastigheter, men det är vid högre denna gör en avsevärd skillnad.

Denna så kallade speciella relativitets teori utgår från två postulat

·         Fysikens lagar är samma för alla som rör sig med konstant hastighet i förhållande till varandra.

·         Ljushastigheten i vakuum är samma för alla som rör sig med konstant hastighet i förhållande till varandra.

Med det första postulatet menas att man inte kan veta vem de är som rör sig. Det är lika korrekt att säga att de är motorvägen som rusar framåt som att säga det är bilen som kör framåt på motorvägen. Med det andra postulatet så klargör det att man kan lita på Michaelson-Morleys experimentet. Man kan tycka att eftersom hela Newtons mekanik är grundad på Galileis relativitetsprincip att Newtons lagar om tillexempel kraft och rörelse inte bör stämma, men trots detta så gör dem faktiskt det till stor del. Om vi mäter och räknar med hastigheter som är låga som dem flesta på vår jord är så fungerar dessa bra. Men om vi räknar med hastigheter nära ljusets hastigheter så blir skillnaderna kolossala.

Tid och avstånd.

Enligt Michelssons och Morleys experiment så upplevs ljushastigheten som den samma oberoende av vilken hastighet som är i förhållande till ljusets källa. Detta experiment är grunden till en hel del intressanta frågeställningar när det handlar om att mäta massor som rör sig i förhållande till den som utför mätningen.

Om vi tänker oss en boll som kastat upp av en pojke i taket på ett tåg och som sedan självklart dras ner av gravitationen tillbaka i pojkens hand. Enligt pojken så har bollen färdats sträckan från hans hand till taket och tillbaka igen likts figur 1.

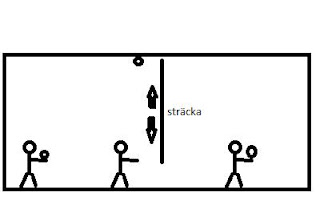
Men om man skulle titta in i tåget utifrån och om samtidigt tåget var i rörelse som pojken kastade bollen så skulle man uppleva sträckan längre likt figur 2.

Eftersom vi ser även tåget röra sig samtidigt som vi ser bollen så blir sträckan annorlunda. Även hastigheten på bollen förändras eftersom även tåget rör sig. Men vi upplever ändå tiden för bollens rörelse den samma.

En annan antagelse man kan gör är att tänka sig ett rymdskepp med en man i som skickar en laserpuls upp mot taket på en rymdfärja. Laserpulsen studsar i sin tur mot en spegel som är fäst i taket och kommer tillbaka till mannen. Mannen har även en klocka som mäter hur lång tid det tar för pulsen att gå till spegeln och tillbaka. Mannen mäter tiden och sträckan laserpusen färdats och konstaterar att ljusets hastighet verkligen är 299792458 m/s. Om vi från jorden skulle se detta så skulle vi precis som exemplet med tåget uppleva att laserpulsen rör sig snett framåt och där av färdats en längre sträcka än vad mannen tycker den gör. Man skulle vilja tro att enligt vårt synsätt rör sig laser pulsen med högre hastighet än enligt pojkens synsätt. Men enligt Einsteins andra postulat så får man inte tro detta. Med detta sagt så verkar det som vi mäter tid eller sträcka olika.

Tidsdilation:

Där t₀ är den tid man mäter om man är still i förhållande till det som mäts, v är hastigheten för det som mäts i förhållande till betraktaren och c är ljushastigheten. Den som observerar något som rör sig tycker det tar längre tid än den som förflyttas tillsammans med det som observeras.

Relativetisk energi:

Där m är föremålets massa och c är ljushastigheten

Kvarkar och leptoner:

Protoner och neutroner byggs upp av endast två sorters kverkar som kallas u (up) respektive d (down).

·         En proton består av två u-kvarkar och en d-kvark. Protonen betecknas p eler (uud)

·         Neutronen består av en u-kvark och två d-kvarkar. Neutronen betecknas n eller (udd).

·         För laddningarna ska stämma måste en u-kvark ha laddningen +2/3 och en d-kvark laddningen -1/3.

All materia byggs upp av kvarkar och leptoner.

·         Kvarkar är tunga och uppträder aldrig fria eftersom de påverkas av den starka kärnkraften. Protonen och neutronen består av kvarkar. Exempel på kvarkar är u-kvark och d-kvark.

·         Leptoner är lätta och uppträder fria eftersom de inte påverkas av den starka kärnkraften. Exempel på leptoner är elektron och neutrino.

Den stabila materien vi ser omkring oss är uppbyggd av tre sorters partiklar, u-kvarkar, d-kvarkar och elektroner.

De tre lagarna

NEWTONS FÖRSTA LAG

Varje kropp förblir i vila eller rörelse med konstant fart längs en rät linje om den inte

Påverkas av en obalanserad kraft.

Bilden ska föreställa en gubbe som sparkar på en boll. I det här exemplet så kommer bollen att röra sig i konstant fart i kraftens riktning om den inte påverkas av en obalanserad kraft. En obalanserad kraft kan tillexempel i detta fall vara gravitationen som kommer att påverka bollen med en kraft nedåt.

NEWTONS ANDRA LAG

F = ma

F betecknar kraft, m massa och a acceleration. (Kraft och acceleration är

vektorstorheter, dvs. storheter som har både storlek och riktning.

NEWTONS TREDJE LAG

Om en kropp påverkar en annan med en given kraft, återverkar den senare kroppen på

Den förra med en lika stor men motsatt riktad kraft.

Välkommen till Fysik 1 for dummies!

Energi och energiresurser 

·         Arbete, effekt, potentiell energi och rörelseenergi för att beskriva olika energiformer: mekanisk, termisk, elektriskt och kemisk energi samt strålnings och kärnenergi.

Arbete

Då ett föremål lyfts finns det några faktorer som påverkar storleken av arbetet. Först och främst hur tungt föremålet är och hur lång sträckan är som föremålet lyfts på. Tyngden på föremålet alltså kraften som krävs för att lyfta det anges som ”F” och sträckan som föremålet lyfts på anges som ”s”. Själva arbetet anges som ”W”.

Definitionen blir alltså 

W = F*s.

SI-enheten är i Newtonmeter (Nm). Kallas vanligen Joule (J)                       

Effekt

Två personer kan utföra samma arbete men en viss skillnad i arbetet kan finnas, beroende anträningen med hur fort de gör det. Skillnaden på arbetet kan beskrivas med storheten ”effekt” (anges som ”p”), detta avser alltså inte bara arbetet som utförs utan även tiden det tar för det.  Ett arbete är alltså jobbigare om det utförs på en minut gentemot om det utförs på 10 minuter.

Formel: 

P = E/t                            effekt = energi/tid = energi per tidsenhet

 

Potentiell energi

Det här skulle kunna ”möjlig” energi likväl, för det är det som ”potentiell” innebär. Det syftar på att energin på något sätt finns lagrad och eventuellt kan användas senare. Lägesenergi är en form av potentiell energi. Ett föremåls läges energi ändras om det lyfts eller sänks. Denna ändring hänger ihop med själva arbetet som utförs under förflyttningen. Tappas någonting i golvet så påverkas det objektet av sin egen tyngd (”mg”) som uträttar ett arbete. Lägesenergin hos objektet omvandlas då till rörelseenergi. Om fallhöjden är ”h” har tyngdkraften uträttat arbetet.

W = F * s = mg * h = mgh

Objektet slår i golvet och just då när den lyfts upp igen, uträttas ett arbete mot tyngdkraften. På så sätt återuppbildas lägesenergin (”mgh”). Ändringen i lägesenergi är detsamma som det utförda arbetet. Energin mäts också i enheten Nm eller (”J”). Detta innebär att på motsvarande sätt medför varje arbete en energiomsättning av samma storlek som arbetet.

Rörelseenergi

Även kallad kinetisk energi. Exempelvis då något objekt släpps från en höjd (”h”) har den en viss rörelseenergi när den når golven. Lägesenergin (”mgh”) omvandlas under fallet till rörelseenergi. Har en boll dubbelt så mycket vikt, så har den enligt formeln dubbelt så stor lägesenergi från starten.  P.g.a. detta borde den ha dubbelt så stor rörelseenergi, eller kinetisk energi (”E_k”). I sådana fall ska rörelseenergin vara proportionell mot massan.

E_k = k₁ * m

Frågan är då hur rörelseenergin beror på hastigheten? Vi kan få en vägledning om sambandet vid undersökning av hur långa bromsträckorna blir för en bil, som bromsas till stillastående från skilda hastigheter. Bromsarbetets storlek blir likvärdigt med hur stor bilens rörelseenergi var från starten. Formeln för att beräkna bromsarbete:

W = F * l

”F” står för bromskraften, alltså kraften från vägen som ”håller emot” däcken. ”l” är bromsträckans längd. Om ”F” är oföränderlig under inbromsningarna, utan hela tiden är den maximala utan att hjulen låser sig. I sådana fall om ”l” blir 40 m är bromsarbetet dubbelt så stort som om ”l” blir 20 m. Bromsarbete – och på så sätt rörelseenergin innan inbromsningen – är proportionellt mot bromsträckan ”l”.

Rörelse och krafter

Hastighet, rörelsemängd och acceleration för att beskriva rörelse.

Krafter som orsak till förändring av hastighet och rörelsemängd. Impuls.

Jämvikt och linjär rörelse i homogena gravitationsfält och elektriska fält.

Tryck, tryckvariationer och Arkimedes princip.

Orientering om Einsteins beskrivning av rörelse vid höga hastigheter: Einsteins postulat, tidsdilatation och relativistisk energi.

Orientering om aktuella modeller för beskrivning av materiens minsta beståndsdelar och av de fundamentala krafterna samt om hur modellerna har vuxit fram.

Hastighet

Ett hjälpmedel när man beräknar hastighet kan vara att rita upp figuren ovan för att kunna se hur man kan ändra om i formlerna. I figuren står (s) för sträcka, (t) för tiden och (v) för hastigheten. Man använder denna genom att man håller för den enhet man vill räkna ut och sedan så gör man vad figuren säger. Ex om vi vill ha fram (t) tar vi sträckan (s) dividerat med tiden (t) enligt formeln t = s/v

Sträcka mäts i meter (m)

Hastighet mäts i meter/sekund (m/s)

Tid mäts i sekunder (s)

Konstant hastighet är den hastighet ett föremål rör sig en viss sträcka under en viss tid.

V=s/t

Medelhastigheten får man genom att beräkna förändringen mellan två hastigheter.

V=s/t

Exempel 1:

Konstant hastighet 
är den hastighet ett föremål rör sig en viss sträcka under en viss tid.

V=s/t

Momentanhastigheten 
(hastigheten vid ett tillfälle) får man genom att beräkna skillnaden mellan två sträckor delat på skillnaden mellan två tider.

∆s/∆t=V

Acceleration

Acceleration mäts i meter/sekund² (m/s²)

Precis som att hastigheten är en förändring av sträckan så är acceleration, som betecknas a, en förändring av hastigheten. 


 a = ∆v / ∆t

Vi kan även räkna ut en hastighet med hjälp av att veta en konstant accelerationen, och tiden multipliceras. Om föremålet har en hastighet före intervallet där hastigheten skall mätas så får vi även addera den till formeln, denna så kallade begynnelsehastighet betecknas v⁰. Hela formeln ser ut så här:

v=v⁰+at

Rörelsemängd
En massa (m) som rör sig med hastigheten (v) har en rörelsemängd (P), som är produkten av massan och hastigheten.

Rörelsemängd:

p = mv

Enhet: 1 kgm/s              

Impuls.

Impulsen säger oss hur mycket rörelsemängden ökar eller minskar hos ett föremål som påverkas av en resulterande kraft under en tidsperiod 

I=F